期权 一个与数学有着不解之缘的工具！

来源：力的期权工作室

π，pi，3.141592653589……一个极其神奇的数字，一个无穷无尽的长河！它绝不仅仅是圆的周长与直径的比值；也是数学界最美的五个数字之一（0，1，pi，e，i）。那么pi与期权之间又有什么关系呢？

如果把“1+1/4+1/9+1/16+……”一直这么加下去，那么最终的结果会等于“pi的平方/6”；

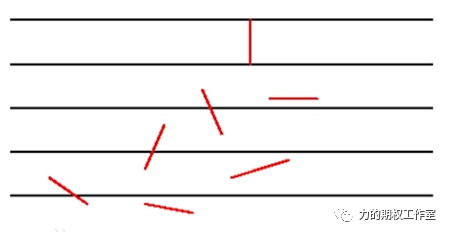
如果画一组间距为A的平行线，把长为L（L<=A）的针随机投到平面上，那么它与平行线相交的概率会等于“（2*L）/（pi*A）”；

任何人的生日序列，比如19900101，它们都能在pi的小数“长河”里找到；

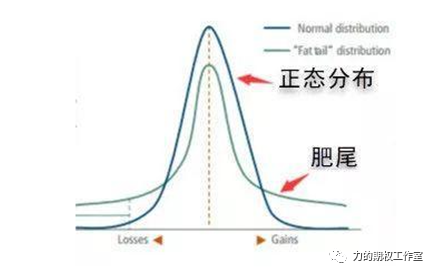
生活中常见的正态分布，金融市场里的肥尾分布，也总能找到pi的踪影；

……

1

期权与π

对于期权这个衍生品，最能和pi扯上关系的莫过于“定价公式”了。

所谓期权定价公式，它是“用来计算一张期权的理论价值究竟是多少”的模型，它的江湖地位就像股票估值里那个“现金流折算模型”一样，当交易所需要确定某些期权的结算价时，当期权做市商们想要确定买卖报价的基准时，都会使用一个相对“权威”的公式，去得出当下认为“合理”的公允价值。

当然，期权定价公式绝不是只有一个喔！不同的假设可以对应不同的公式，不同类型的期权也可以对应不同的公式，欧式期权有欧式的定价公式，美式期权也有美式的定价公式，然而不论如何，绝大多数的定价公式里都会隐藏着圆周率“pi”的踪迹。

比如，对于欧式期权，最为经典的“Black-Scholes定价模型”就包含了圆周率，它的公式形状如下：

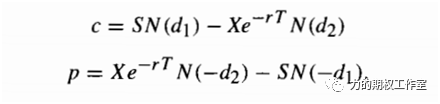
其中，S就是标的价格，r是无风险利率，X是期权的行权价格，T表示距离到期的年化时间（如距离到期还有一周，则T=7/365=0.0192），d1和d2则如下所示：

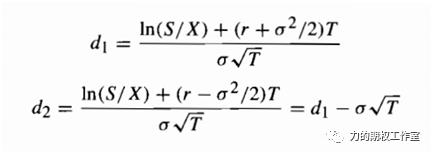
整个模型中，N（．）就是正态分布函数，在Excel单元格里可以用normdist去计算，在Matlab里可以用normcdf去计算，正是因为正态分布函数的存在，使得每一份期权的公允定价里包含了pi的踪迹。

还记得去年4月中旬的“奇观”吗？WTI原油期货价格一度为负，芝商所（CME Group）在紧急情况下竟然搬出了压箱底的、“远古时期”的“Bachelier定价模型”（1900年）来发布每天的期权结算价。

同样地，在Bachelier期权定价公式中，也是由于正态分布函数的存在，我们同样找到了圆周率pi的踪迹。

图：Bachelier期权价格公式

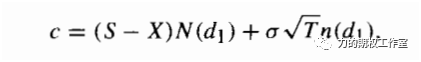
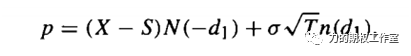
这里的N（．）同样是正态分布函数，S、X同样表示标的价格和期权的行权价格，d1的含义则如下所示：

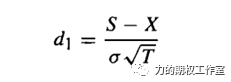
2

期权与数学世界

当然，期权不仅和圆周率有关，它更与整个数学世界有着不解之缘！

比如奇函数的导数是偶函数，偶函数的导数是奇函数，这样的一个数学原理就可以体现在Delta、Gamma这些希腊字母的图形上。

我们知道，期权是标的资产的衍生产品，两者之间就像是“父子关系”一样，父亲的一举一动每时每刻都在影响着孩子的行为，父亲的这种影响力就可以认为是Delta。

认购期权像一个“乖孩子”，它的delta大于0，在方向的维度上，总是喜欢与父亲同调，而认沽期权则恰恰相反，像一个“坏孩子”，它的delta小于0，在方向的维度上，总是喜欢和父亲拧着来，可是，不管是“乖孩子”还是“坏孩子”，他们受到父亲的影响力并非是一成不变的，而Gamma正是用来描述父亲影响力变化的，即标的价格变化一个单位，期权的Delta会变化多少。

以单腿买入认购期权为例：

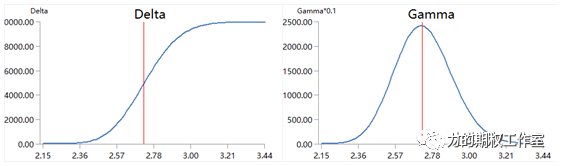
在上图中，我们发现Delta的图形是中心对称的，非常类似我们高中时代提及的奇函数，而Gamma的图形呢，它是轴对称的，非常类似以前学过的偶函数。

由于Gamma可以看成是Delta的一阶导数，于是，我们立刻可以联系到这样的一个原理——“奇函数的一阶导数是偶函数，偶函数的一阶导数是奇函数”，基于这个原理，我们就可以根据任何一种期权组合Delta的图形，极速地画出这一组合的Gamma图形。

举两个例子，比如，下图左侧是牛市价差策略的Delta图形，它像什么？是不是形状上很像cos（x）余弦函数那样的偶函数，于是牛市价差策略的Gamma图形就会很像右侧所示的，形似sin（x）正弦函数那样的奇函数。图：牛市价差组合的delta、gamma图形

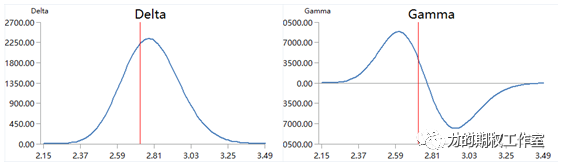
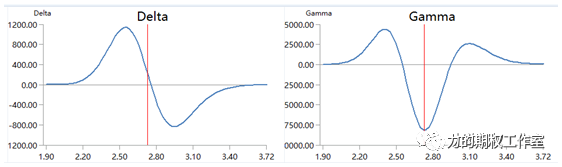
又如，下图左侧是正向日历策略的Delta图形，它像什么？是不是很像sin（x）正弦函数那样的奇函数，于是正向日历策略的Gamma图形就会像右侧所示的，形似cos（x）余弦函数那样的偶函数。

图：正向日历策略的delta、gamma图形

3

期权的“隐波”

当然，期权和数学的关系里怎能少得了“隐波”这个指标……

期权的隐含波动率，一个类似于“股票市盈率”的变量，每个合约就像每个股票一样，都有着自己的“市盈率”（隐含波动率），然而，每个合约的隐含波动率之间绝不会毫无约束，否则就会出现套利机会，在高频交易者面前会被迅速抹平。

那么，不同期权的隐含波动率之间有什么数量关系彼此约束呢？我们至少可以总结四点：

第一，同一月份不同行权价的认购、认沽期权价格一般是单调的，行权价越高，认购期权价格越低，认沽期权价格则越高，如果某份期权的隐含波动率高的或者低的离谱，导致这个数量关系被违反了，那么“低买高卖”的套利机会便随之产生了。

第二，同一行权价的远月期权价格一般是高于近月期权价格，这和保险费的原理是一样的，对于同一个被保资产，买一份1年期的保险对比买一份3个月的保险，保险费一定是前者比较贵！如果近月期权的隐含波动率高的离谱，导致近月期权的价格高于了相同行权价的远月期权，那么“卖近买远”的操作也就可以一触即发。

第三，同一行权价、同一到期月份认购和认沽之间的价格也不会随心所欲，它们要大致地满足一个公式（Put-Call Parity），那就是：认购价格+行权价的贴现值=标的价格+认沽价格。如果认购或认沽期权其中一个的隐含波动率出现剧烈上升或下降，这个等式就会失去平衡，套利机会也会随之产生

第四，则是三角关系的约束，同一月份，三个不同行权价的认购（或认沽）期权的价格需要满足一个叫做凸性的不等式，比如，“中间行权价的期权价格*2倍”一定要小于“两侧行权价的期权价格之和”，如果这个不等式被违反了，则这三个合约就会变成套利者的“美食”！

……

在期权的世界里，无处不在的数学原理还有很多……，这些内在规律体现了数学的魅力，而这种魅力也让期权无愧于衍生品皇冠上的那颗明珠。

　　版权及免责声明：凡本网所属版权作品，转载时须获得授权并注明来源“融道中国”，违者本网将保留追究其相关法律责任的权力。凡转载文章，不代表本网观点和立场。

延伸阅读